トピックモデルで単語の分散表現 - 理論編

こんにちは。代表の島田です。最近はDeepLearningがホットなキーワードになっていますが、トピックモデルという自然言語処理における手法も、少し前に注目を集めました。聞いたことはあるけど何なのかわからない、という方のために、今回はトピックモデルに関して説明します。 Pythonなどの言語ではライブラリが利用できますが、トピックモデルなどの原理を知っておくことでパラメータチューニングが思いのままにできるようになります。

LDAやトピックモデルについては最新の技術！というわけではないので他にも解説記事があると思いますが、今回は「流行りの単語がとりあえず何なのか知る」ということを目的に、前半は機械学習エンジニアではない方にもわかりやすく解説しようと思います。

モチベーション

単語をベクトルで表したい！

自然言語データを使ったレコメンドエンジンの構築やテキストの分類などで、単語をクラスタリング（意味の似ているグループごとに分ける）や DeepLearningを使って識別したいというシーンはよく見かけます。しかし、「りんご」「コンピューター」といった単語そのままという形では、DeepLearningなどのような手法に入力することが出来ません。そこで、コンピューターでもわかるように単語を「ベクトル」という形式に変換してあげる必要があります。その形に変換することで、いろんな分析手法を適用することができますが、その方法は簡単ではありません。研究者によっていろいろな方法が提案されてきました。

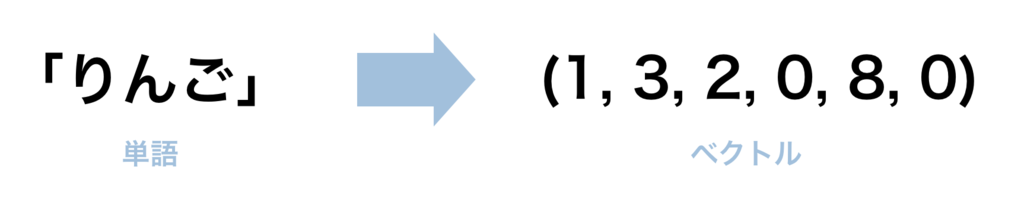
局所表現と分散表現

Deep Learningの登場以前は、単語をベクトルで表す方法は、ボキャブラリーサイズ（扱う全単語の数）の次元数を持ち、該当インデックスだけ1で他の値が0というone-hotベクトル（1つの概念を1つの成分で表すので局所表現という）が使われていました。次に、「もし、2つの単語が似ている文脈（つまりその単語の周りの単語のこと）で使われているなら、その単語は似ている」というDistributional Hypothesis に基いて、単語を、その単語と同時に使われる単語たちの生起回数でベクトル表現する（これは複数の成分で概念を表現しているので分散表現という）という共起表現が現れましたが、この方法でもベクトルの次元が（同じくボキャブラリーサイズなので）大きくなりすぎ、かつスパース（0が多すぎる）になってしまうため問題がありました。

そこで、せいぜい100〜200次元くらいの低次元ベクトルでひとつの単語の意味を表現するにはどうしたら良いか？という問が生まれ、Deep Learningの流行と相まって近年いろいろな手法が生まれました。Word2Vecで使われているSkip-Gramなどは主流ですが、このシリーズ記事では、そのやり方の一つであるトピックモデル（とLDA）を用いて単語の分散表現を作ることについて解説します。今回の理論編では、トピックモデルとLDAの基礎理論について解説します。

トピックモデル・LDAとは

トピックモデルは、大雑把に言い表わせば文書にトピック（その文書のジャンル・カテゴリ）を教師無しで割り当てる手法のことです。トピックモデルにおいては、予め指定しておかなければならない変数はトピックの数のみで、それぞれのトピックが何なのか（「政治」とか「スポーツ」とか）は指定したり登録したりする必要が無いので、非常に便利です。なぜなら、トピックというのは「政治」とか「スポーツ」とかいった人間からみたジャンルではなく、単語の分布として表わされるからです。

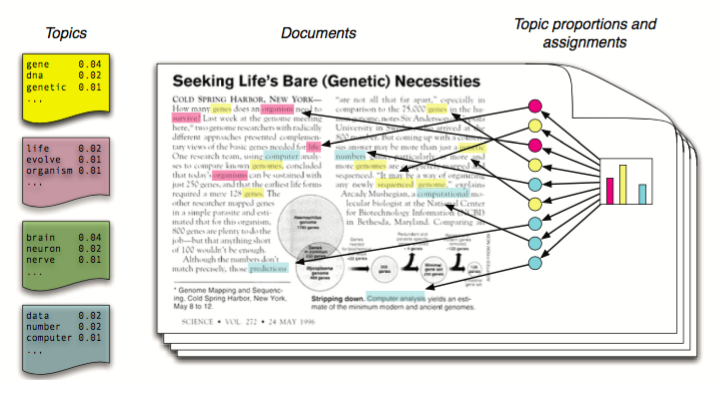
上図([1] より引用)では1番目のTopic(黄色) が gene, dna, genetic という単語をトップに含んでいるトピック（つまり遺伝子関係のトピック）で、3番めのTopic（緑）がbrain, neuron, nerveを含んでるトピック（脳に関するトピック）を表す。左に出ているのがすべてのトピックなら、トピック数は4で、この文書は4次元のベクトルで表されます。

つまり、各トピックは、感覚的には「単語のブレンド」という感じで表されます。そして、各単語は、各トピックにどれくらいの確率で属すか？という「トピックのブレンド」で表されます。

LDA（Latent Dirichlet Allocation）とは、トピックモデルに用いられる代表的な確率モデルで、LDAそのものは文書生成モデルです。この確率分布を使って文書にトピックを教師なしで割り当てるのが、トピックモデルです。

基本構造：もう少し詳しく

LDAそのものは文書の生成モデルです。つまり、与えられた文書がLDAによって生成されると仮定したときのその文書の生成確率を計算したいために、生成モデルを考える必要がある、ということです。 LDAでは以下の流れで文書を生成します。

文書の単語数Nとトピックの数Tを決める
例) N=4, T=2
各トピック$j$ごとの単語の分布$\boldsymbol{\phi^{(j)}}$をDirichlet分布$Dir(\beta)$に従って決める。
各文書$d$における(単語の)トピックの分布$\boldsymbol{\theta}^{(d)}$をDirichlet分布(ディリクレ分布) $Dir(\alpha)$に従って決める
例) 1/2 の確率でfoodカテゴリ, 1/2の確率でanimalカテゴリになる分布とする
以下の手順で文書d内のN個の単語を生成
1. トピック分布$\boldsymbol{\theta}^{(d)}$に従ってd内の単語のトピックを、T個のトピックの中から1個選ぶ
  例) T1 = food, T2=animal, T3=animal, T4=food
2. $\boldsymbol{\phi}^{(j)}$に従って、先の手順で選んだ各トピックに基いて文書内の単語を決める。
  例) w1=broccoli, C2=panda, C3=bird, C4=eating

Dirichlet分布はベータ分布の多変数版にあたる分布で、適当なパラメータを与えて分布を生成できるので、確率分布の確率分布として扱われます。一般式は次のように与えられます。

$$P(\boldsymbol{\theta}) = \frac{1}{Z}\prod_{j=1}^K \theta_j^{\alpha_j -1}$$
また、表記上、$Dir(\alpha, \cdots, \alpha) = Dir(\alpha)$と書きます。 $\alpha$は文書中のトピック分布を平滑化する役割を持っていて、小さいほど(0.01~0.1)分布が際立ち、大きいほど（10〜）分布がなめらかになる（トピックごとの確率差がなくなる）。

そして、上でいう$\boldsymbol{\theta}, \boldsymbol{\phi}$は次の学習プロセス、従ってデータから学習することで得ることができます。

各文書を見ていき、その文書の中の単語をひとつづつランダムにT個のトピックのうちどれかに割り当てる。（初期値として）
各文書を見ていき、その文書$d$の中の単語$w$と各トピック$t$について、以下を計算する
- $p(t|d)$：文書$d$中のトピック$t$の単語数 / 文書$d$の全単語数。つまり$\boldsymbol{\theta}^{(d)}_j$ にあたる。
- $p(w|t)$：トピック$t$内での単語$w$の数 / トピック$t$の全単語数。つまり$\boldsymbol{\phi}^{(j)}_i$ にあたる。
手順2で計算した確率の積 $p(w|t) * p(t|d)$ が、をもとに、$w$に新しいトピックを割り当てていく。
2の確率が変化しなくなるまで2と3を十分繰り返す。

なんというか、クラスタリングに似ていますね。この手順で最終的に得られた$p(t|d)$と$p(w|t)$は、先に説明した手順の生成モデルで文章が生成されると仮定されたときのトピック分布と単語の分布ということになります。この$p(t|d)$が、文書を表すトピックのベクトル（次元数はトピックの数に等しい）となります。

LDAでどう単語の分散表現を作るのか？

LDAは、文書（単語の集合）が与えられた時に、その文書が属するトピックを推測するものでした。従って、クラスタリングに用いられることが多いのですが、これを使って単語の分散表現を作ることもできます。 LDAが文書に対する手法ならば、ある単語の共起表現ベクトル（一緒に使われた回数を格納したベクトル。次元数は単語数）を一つの文書（頻度と同じ数だけ単語が含まれている文章。単語順は考慮しない。）と見立て、それに対しLDAを適用すればよいということです。共起表現ベクトルはそのままだと次元数が巨大過ぎてスパースになりやすいですが、LDAを使えば適当な次元（100~500くらい？）に次元縮約することができる。つまり、トピックモデルをBoWや共起表現ベクトルに使うことによって、次元縮約器としてはたらく、ということになります！

次回記事では、Pythonのライブラリgensimを用いて、この方法によって実際に分散表現を作ることを解説します。

参考文献

[1] Griffiths, Thomas L., Mark Steyvers, and Joshua B. Tenenbaum. 2007. Topics in semantic representation. Psychological Review 114(2):211–244.

トピックモデルで単語の分散表現 – 理論編