scoutyの高濱です。本記事では、インターンの田村くんと協力してscoutyでの転職可能性予測ロジックに組み込んだ生存時間解析に関する基礎的な事項の説明を行います。 転職可能性予測は、こちらの記事の通り、候補者の現在の転職の可能性を推定して提示し、スカウトメールを送るか否かの判断を助けます。 生存時間解析は、予測ロジックのコンポーネントのひとつとして、経歴などの情報から候補者が現職を退職する時期(月単位)を予測するために利用されています。
生存時間解析とは
生存時間解析とは、生物の死亡や機械系の故障など、一つまたは複数の事象(イベント)が起こるまでの予想される時間を分析するための一般化線形モデルの一分野です。分野によって様々な呼び方があり、例えば工学では信頼性分析 (reliability analysis)、経済学では期間分析 (duration analysis)、社会学ではイベント分析 (event history analysis) などと呼ばれます。
具体的には、各分野で以下のような時間に関する分析を与える際に生存時間解析が用いられます。
- 労働経済学: 就職してから離職に至るまでの時間。
- 機械工学: 機械が使われ始めてから正常に動作しなくなるまでの時間。
- 医療: ある疾患と診断されてから死亡するまでの時間。
- Webサービス: 会員登録から離脱までの時間。
このうち、最初に挙げた「就職してから離職に至るまでの時間」は、scoutyで転職可能性予測を行う際にまさに分析の対象としたいものに該当します。本記事では、生存時間解析の基礎に関する解説を行います。
関数名とその定義
最初に、生存関数 \(S(t)\), 死亡関数 \(F(t)\), ハザード関数 \(h(t)\) をそれぞれ紹介します。これらの、時間 \(t\) に関する関数は生存時間解析のモデルを決定づけるもので、このうち一つでも定まればその他の関数を比較的容易に導出することができます。そのため、生存時間をモデリングする場合は通常、生存(死亡)関数もしくはハザード関数を仮定したのち、パラメータ推定に必要なその他の関数を計算するという手順を踏みます。
以下では、 \(T\) は生存時間の確率変数、 \(t>0\) は生存時間の実現値、 \(f\) は生存時間の確率密度関数を表します。
ハザード関数 (hazard function)
ハザード関数とは、時間 \(t\) までは生存しているという条件のもとで、\(t\) と \(t + \delta t\) の間に死亡する確率を表す関数で、十分小さい値 \(\Delta t\) を用いて以下のように定義されます。
$$\begin{align*}
h(t) = \lim _{\Delta t \rightarrow 0} \frac{\mathrm{Pr}( {t \le T < t + \Delta t} \ | \ { T \ge t }) }{\Delta t}
\end{align*}$$
一例として、よく使われるパラメトリックモデルであるワイブル回帰モデルでのハザード関数( \(\lambda = 1.5\) として、 \(\theta\) を動かしたもの)は以下のようになります。
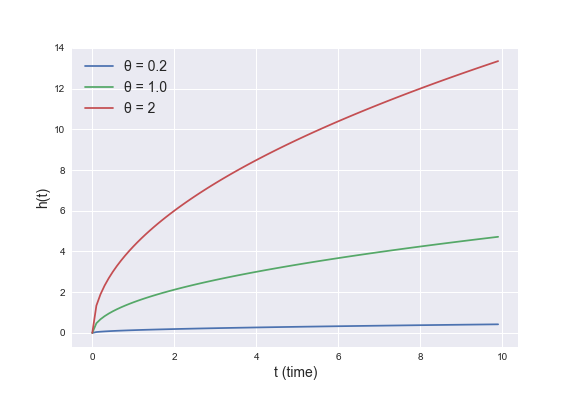
図1: ワイブル分布 (λ = 1.5) のハザード関数
\(h(t)\) はパラメータ推定などの式変形には現れませんが、モデリングする際のドメイン知識の埋め込みに有効である場合があります。例えば、ある機械はその使用年月に応じて疲労が蓄積するため、故障の確率は徐々に高まっていくことが知られていたとします。この機械に対する生存時間分析を行う際には、単調増加なハザード関数を仮定することで故障に関する知見をモデリングに反映することができます。
生存関数 (survival function)
ある時間 \(t\) 以上生存する確率を表す生存関数 \(S(t)\) は以下のように定義されます。
$$\begin{align*}
S(t) = \mathrm{Pr}( T \ge t) = \int_t^\infty f(u)\mathrm{d}u
\end{align*}$$
\(f(t) \ge 0\) が常に成り立つことから、 \(S(t)\) は単調減少な関数です。 一例として、よく使われるパラメトリックモデルであるワイブル回帰モデルでの生存関数( \(\lambda = 1.5\) として、 \(\theta\) を動かしたもの)は以下のようになります。
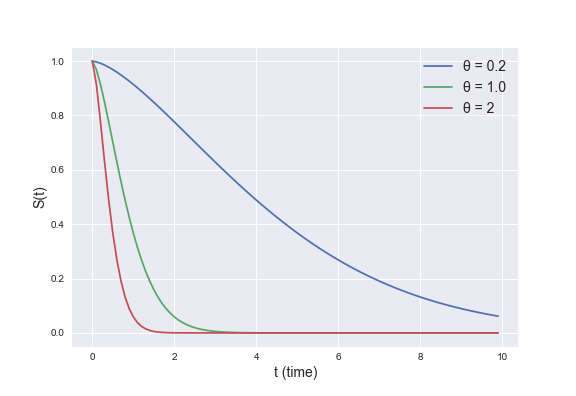
図2: ワイブル分布 (λ = 1.5) の生存関数
図2は図1に対応しています。先述のハザード関数がある時点での死亡率に該当する値をもつことを考慮すると、 \(\theta\) が大きくなればなるほど死亡しやすさが大きくなると解釈できるので、生存関数は早い段階で0に近づきます。
\(F(t) = 1 - S(t)\) によって定義される \(F(t)\) を死亡関数と呼びます。 \(t: 0 \rightarrow \infty\) のとき \(S(t): 1 \rightarrow 0\) ですから、 \(F(t)\) は \(t: 0 \rightarrow \infty\) のとき \(F(t): 0 \rightarrow 1\) となる単調増加な関数で、 \(y=0.5\) を軸にして \(S(t)\) を上下反転させた形になります。
関数間の関係
先述した通り、生存関数 \(S(t)\), 死亡関数 \(F(t)\), ハザード関数 \(h(t)\), 確率密度関数 \(f(t)\) は、このうち一つが決定されるとその他の関数を容易に導出することができます。これらの関数に関してよく用いられる関係式を記載します。
$$\begin{align*}
S(t) = \int_t^\infty f(u)\mathrm{d}u, \ \ f(t) = - \frac{\mathrm{d}}{\mathrm{d}t}S(t)
\end{align*}$$
$$\begin{align*}
f(t) = h(t) \times S(t), \ \ h(t) = \frac{f(t)} {S(t)}
\end{align*}$$
$$\begin{align*}
F(t) = 1 - S(t)
\end{align*}$$
データの形式について
打切り (censoring)
生存時間解析では、しばしば打切りが発生したデータを扱います。例えば、がん患者の生存時間を調査するとき、実際にデータ収集を行う場合を考えると、現実的には調査対象の患者の状態を永久に追跡し続けることは不可能であるため、調査期間が限定されてしまう状況を想定するのが自然です。そのため、収集されたデータには、調査期間中に死亡する患者に関するデータと、調査期間が終了するまでに死亡しなかった患者に関するデータが共に存在することになります。
もし観察対象(患者、従業員、機械など)の観察期間中にイベント(死亡、退職、故障など)が発生しなかった場合、打切りデータとして記録されます。打切りデータには、以下のような種類があります。
- 右側打切り (right censored): 観察期間終了までにイベントが発生しなかった場合。
- 左側打切り (left censored): 観察期間開始前にイベントが発生していた場合。
- 中間打切り (interval censored): 2つの観察期間で挟まれた非観察期間にイベントが発生した場合。
特によく扱われるのは右側打切りデータであるため、本記事でも特に断りがない場合は打切りデータとして右側打切りのみを扱うこととします。
一般的なデータフォーマット
生存時間解析では以下のようなデータフォーマットを扱うことが多いです。
id |
生存時間 (t) |
打切り (censored) |
|---|---|---|
| 1243 | 4 | False |
| 2389 | 20 | True |
| 1289 | 6 | False |
| 4389 | 12 | False |
上表に示したデータを用いて、ある群の死亡に関する傾向を発見するのが最も基本的な生存時間解析です。また、これに加えて各 id の特徴量(例えば、ある人の年齢・身長・体重・病歴*1など)を考慮した解析を行うように拡張することもできます。
パラメータ推定方法の概要
生存時間解析では、基本的に生存関数 \(S(t)\) や確率密度関数 \(f(t)\) に含まれているパラメータを最尤推定によって求めることで学習を行います。 \(S(t)\) や \(f(t)\) に仮定する関数形によって推定の手順が変化しますが、本節ではどのモデルの最尤推定でも共通して必要な(対数)尤度関数の定義について述べます。
一般的な最尤推定と異なり、生存時間解析では用いるデータに打切りが存在することを容認するため、尤度関数が多少複雑になります。先に述べた右側打切りを考慮した尤度関数の定義は以下のようになります。
$$\begin{align*}
L(\theta) = \prod_{ i \ \in \ \mathrm{unc.} } \mathrm{Pr}( T = t_{i} ; \theta ) \times \prod_{i \ \in \ \mathrm{csd.}}\mathrm{Pr}( T > t_{i} ; \theta )
\end{align*}$$
ここで、式中の各変数が表す内容は以下のようになります。
- \(L( \theta )\): 尤度関数。最尤推定によって求めたい全てのパラメータを便宜的に \(\theta\) で表現しています。
- \(\mathrm{unc.}\): 非打切り (uncensored) データからなる集合。
- \(\mathrm{csd.}\): 打切り (censored) データからなる集合。
さて、非打切りデータに対して用いる \(\mathrm{Pr}( T = t_{i} ; \theta )\) の意味を考えると、打切りが発生しなかったため、尤度として「 \(i\) がちょうど時間 \(t_i\) で死亡する確率」を用いるのが適切なので、以下のように密度関数 \(f(t)\) を用いて表現されます*2。
$$\begin{align*}
\mathrm{Pr} ( T = t_{i} ; \theta ) = f ( t_{i} ; \theta )
\end{align*}$$
次に、打切りデータに対して用いる \(\mathrm{Pr}( T > t_{i} ; \theta )\) の意味を考えると、 \(t_i\) の時点で打切りが発生したため、尤度として「 \(i\) が少なくとも時点 \(t_i\) まで生存する確率」を用いるのが適切なので、以下のように生存関数 \(S(t)\) を用いて表現されます。
$$\begin{align*}
\mathrm{Pr} ( T > t_{i} ; \theta ) = S( t_{i} ; \theta )
\end{align*}$$
では、 \(f(t)\), \(S(t)\) を用いて尤度関数を書き直します。さらに、サンプル \(i\) が打切りデータである場合は \(c_i = 0\), 非打切りデータである場合は \(c_i = 1\) となるような変数 \(c_i\) を用いて、尤度関数 \(L(\theta)\) を以下のように簡略に表すことができます*3。
$$\begin{align*}
L(\theta) = \prod_{i = 1}^{N} \left\{ f ( t_{i} ; \theta )^{c_i} \times S( t_{i} ; \theta )^{1 - c_i} \right\}
\end{align*}$$
最後に、最尤推定ではしばしば尤度関数の最大化のために対数尤度関数を扱うので、上式に対応する対数尤度関数もここで計算しておきます。
$$\begin{align*}
\ln L(\theta) = \sum_{i = 1}^{N} \left\{c_i \ln f ( t_{i} ; \theta ) + (1 - c_i) \ln S( t_{i} ; \theta ) \right\}
\end{align*}$$
実際のパラメータ推定では、対数尤度関数 \(\ln L(\theta)\) の \(\theta\) に関する微分を計算することで \(\ln L(\theta)\) を最大化する \(\theta\) を求めます。
生存時間解析で利用されるモデルの分類
生存時間解析でよく利用されるモデルは大きく(完全)パラメトリックなモデルとセミパラメトリックなモデルに分かれます。
パラメトリックなモデル
パラメトリックなモデルはハザード関数の形を陽に仮定します。一例として、特によく用いられる指数回帰モデルとワイブル回帰モデルについては、ハザード関数 \(h(t)\), 生存関数 \(S(t)\), 確率密度関数 \(f(t)\) は以下のように定義されます。
| モデル | ハザード関数 \(h(t)\) | 生存関数 \(S(t)\) | 確率密度関数 \(f(t)\) |
|---|---|---|---|
| 指数回帰モデル | \(\theta\) | \(e^{-\theta t}\) | \(\theta e^{-\theta t}\) |
| ワイブル回帰モデル | \(\theta \lambda (\theta t)^{\lambda - 1}\) | \(e^{-(\theta t)^\lambda}\) | \(\theta \lambda (\theta t)^{\lambda - 1} e^{-(\theta t)^\lambda}\) |
ここで、関数中の \(\theta > 0\), \(\lambda > 0\) は分布の形を決めるパラメータで、学習データを用いて上述した最尤推定を行うことで決定されます。なお、ワイブル回帰モデルは指数回帰モデルの一般化であり、ワイブル回帰モデルで \(\lambda = 1\) とすれば各式は実際に指数回帰モデルの式と一致します。
これらの分布の特徴、導関数の導出、パラメータの推定、拡張の方法などについては別記事で詳細に解説します。
セミパラメトリックなモデル
セミパラメトリックなモデルでは、モデルを決定づける関数群は以下のように定義されます。
- ハザード関数 \(h(t) = h_0(t) r(\boldsymbol{x}, \boldsymbol{\beta}) \ \ (> 0)\)
- \(h_0(t)\): 基準ハザード関数
- \(r(\boldsymbol{x}, \boldsymbol{\beta})\): \(\boldsymbol{x}\) および \(\boldsymbol{\beta}\) に依存する何らかの関数
- \(\boldsymbol{x}\): サンプルの特徴ベクトル
- \(\boldsymbol{\beta}\): 各特徴に対する重みベクトル
- 累積ハザード関数\(H(t, \boldsymbol{x}, \boldsymbol{\beta}) = r(\boldsymbol{x}, \boldsymbol{\beta}) H_0(t)\)
- \(H_0(t) = \int_0^t h_0(u) \mathrm{d}u\): 累積基準ハザード関数
- 生存関数\(S(t) = \left[ S_0(t) \right]^{r(\boldsymbol{x}, \boldsymbol{\beta})}\)
- \(S_0(t) = e^{-H_0(t)}\): 基準生存関数
パラメトリックなモデルとの本質的な違いとして、セミパラメトリックなモデルでは \(h_0(t)\) の関数形を仮定しません。学習データに含まれるサンプルが「いつ死亡したか」「いつ観察が打ち切られたか」という情報から求められる生存関数の推定量*4のうち最もよく用いられる Kaplan-Meier 推定量の考え方をもとにして \(h_0(t)\) を決定します。
ちなみに、サンプルの特徴 \(\boldsymbol{x}\) を明示的に考慮することを前提としたモデルなので、その点も異なっているように見えますが、パラメトリックなモデルを \(\boldsymbol{x}\) を考慮するように拡張することもできるので、この部分はパラメトリックなモデルに対する本質的なアドバンテージであるというわけではありません。
セミパラメトリックなモデルのうち、最もよく用いられるCox比例ハザードモデルでは \(r(\boldsymbol{x}, \boldsymbol{\beta}) = \exp(\boldsymbol{\beta}^\top\boldsymbol{x})\) を利用します。
先に述べた対数尤度関数にCox比例ハザードモデルの生存関数と確率密度関数を代入して得られるものを完全尤度関数 (full likelihood function) と呼びますが、完全尤度関数の直接の最大化は不可能である [Kalbfleisch and Prentice] とのことで、実際には以下の処理を順に行うことでパラメータの推定を行います。
- 部分尤度関数 (partial likelihood function) の最大化によって \(\boldsymbol{\beta}\) を推定
- 求まった \(\boldsymbol{\beta}\) を使って基準生存関数 \(S_0(t)\) に関する尤度を計算して最大化し、 \(S_0(t)\) を推定
- 求まった \(S_0(t)\) から基準ハザード関数 \(h_0(t)\) を推定
Cox比例ハザードモデルに関するパラメータ推定の方法についても別記事で扱うこととします。
パラメトリック/セミパラメトリックの使い分けについて
モデリングを行う対象の死亡率が時間によってどのように変化するかについて非常に詳細に分かっている場合はパラメトリックなモデルが非常に効果的です。すでに知られている観察対象のふるまいをよく表現するハザード関数をもつようなモデルを選択することで、ドメイン知識を適切にモデルに取り込むことができます。 一方、ハザード関数に対しての事前情報に乏しい場合、複雑なパラメトリックモデルを使うべきではなく、セミパラメトリックなモデルを利用するのが無難であるといえます。
おわりに
本記事では生存時間解析の全体を俯瞰するために、用語の説明とモデルの簡単な説明を行いました。 重要な各モデルの詳細な解説は、今後に公開する記事中で行いますので、そちらをご参照ください。
参考文献
- John D. Kalbfleisch and Ross L. Prentice, "The Statistical Analysis of Failure Time Data", 2nd Edition (2002).
- David W. Hosmer, Stanley Lemeshow and Susanne May, "Applied Survival Analysis: Regression Modeling of Time-to-Event Data", 2nd Edition (2008).
脚注
*1: 例えば、高血圧と診断されたことがあるか否かを表現する二値の特徴などが考えられます。
*2: \(f(t)\) は密度関数なので、厳密には確率ではありませんが、\(f(t) = \lim_{\Delta t \rightarrow 0} (F(t + \Delta t) - F(t) ) / \Delta t\) であるとしてこれが用いられるようです。
*3: この表現が業界では一般的なようですが、 \(c\) が censored の略であることを考えると、 \(\mathrm{censored} = 1 (= \mathrm{True})\) を打切りデータに対応させるべきでは?(論理値逆転してないか?)という気持ち悪さがあります...。
*4: 「生存関数の推定量」という表現は微妙ですが、ある期間 \(t_i\) (たとえば 20ヶ月目から22ヶ月目 というような範囲)で一定となるような値を全て推定するようなイメージです。
