scoutyの高濱です。本記事では、生存時間解析におけるノンパラメトリックな推定量のうち代表的なものである Kaplan-Meier 推定量と Nelson-Aalen 推定量について紹介します。
生存時間解析の概要については以下の記事をご参照ください。
上の記事で紹介しましたが、生存時間解析では、モデルの形状をどの程度の強さで仮定するかに依存して、モデルの種類が仮定が強い順に「フルパラメトリック」「セミパラメトリック」「ノンパラメトリック」に分類されます。 しかし、個別のサンプル*1の特徴量*2をモデルに含めるか否かについての表現がさまざまな文献でしばしば雑に扱われ、読者の混乱を招いていると認識しています*3。 具体的には、セミパラメトリックなモデルの多くは上述した特徴量を明示的に含む表現が使われがちである一方、フルパラメトリックなモデルに関しては、特徴量を含む前提で説明されている場合と含まない前提で説明されている場合があります。
それに対して、今回紹介するノンパラメトリック推定では、基本的に特徴量を含まない表現しか使われません。 このため、ノンパラメトリック推定は、ある母集団についてすでに知られたハザードと観測された生存時間データの間の差、あるいは複数の生存時間データの集団ごとの差の有無に関して検定を行うために用いることはできますが、 scoutyでの利用目的である「ある候補者の転職時期を予測したい」といった予測モデリングのニーズに応えることを想定した手法ではありません*4。
以上を考慮し、ノンパラメトリックな手法については検定に関する事項などまで深くは立ち入らず、推定量の存在とその定義について簡単に紹介するに留めたいと思います。
ノンパラメトリック推定
本章では、生存関数 \(S(t)\) の推定量である Kaplan-Meier 推定量と累積ハザード関数 \(H(t)\) の推定量である Nelson-Aalen 推定量を紹介します。
以下では、 [Klein and Moeschberger] で紹介されている、急性白血病の臨床試験からの寛解持続時間に関するデータセット [Friereich et al.] のうち、抗癌剤を投与された患者に関する生存時間データ 6-MP を用いて関数の推定量の描画の例を示します。 6-MPはデータ数21件の小さなデータセットで、生存時間を示す time と、打ち切りか否かを示す censored からなります:
| id | time | censored |
|---|---|---|
| 1 | 10 | False |
| 2 | 7 | False |
| 3 | 32 | True |
| 4 | 23 | False |
| 5 | 22 | False |
| 6 | 6 | False |
| 7 | 16 | False |
| 8 | 34 | True |
| 9 | 32 | True |
| 10 | 25 | True |
| 11 | 11 | True |
| 12 | 20 | True |
| 13 | 19 | True |
| 14 | 6 | False |
| 15 | 17 | True |
| 16 | 35 | True |
| 17 | 6 | False |
| 18 | 13 | False |
| 19 | 9 | True |
| 20 | 6 | True |
| 21 | 10 | True |
推定量を定義するに際して必要な変数を定義します。 打ち切られたものを含まない死亡のイベントが \(D\) 個の異なる時間 \(t_1 < t_2 < \dots < t_D\) で発生し、各時間 \(t_i\) では \(d_i\) 人が死亡しているとします。 また、時間 \(t_i\) において死亡する可能性がある対象者数を \(Y_i\) します。 \(Y_i\) は、時間が経つに従って対象者が死亡したり観測が打ち切られたりすることで減少していきます。
Kaplan-Meier 推定量
Kaplan と Meier によって提案された生存関数 \(S(t)\) の推定量 \(\hat{S}(t)\) は Kaplan-Meier 推定量*5と呼ばれ、以下のように定義されます:
$$\begin{align*}
\hat{S}(t) = \left\{
\begin{array}{ll}
1 \displaystyle\frac{\mbox{}}{\mbox{}}& (\mathrm{if} \quad t < t_1) \\
\displaystyle\prod_{i = t_1}^t \left(1 - \frac{d_{i}}{Y_{i}} \right) & (\mathrm{if} \quad t_1 \le t)\end{array}
\right.
\end{align*}$$
6-MPに対する Kaplan-Meier 推定量をプロットすると以下のようになります:
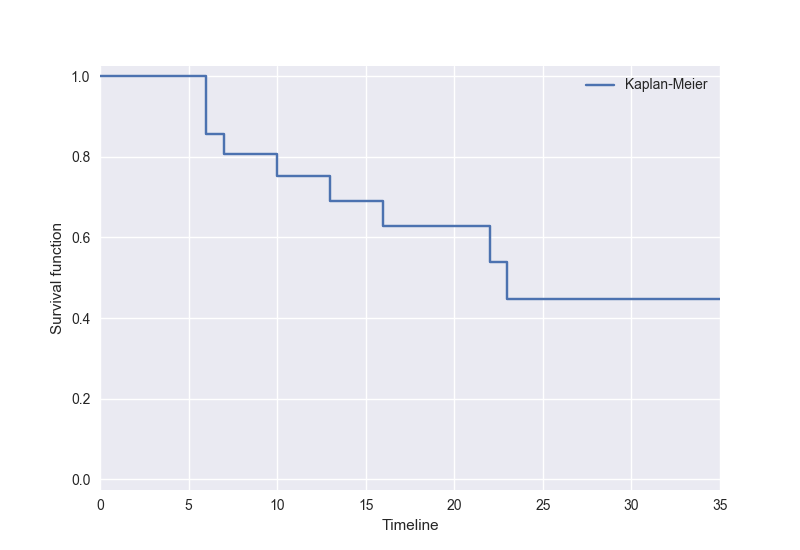
変数及び Kaplan-Meier 推定量の定義から明らかですが、Kaplan-Meier 推定量は 1 からスタートし、誰かの死亡が観測された時点で値が小さくなるような階段関数です。
前記事でも述べた通り、生存関数は \(S(t)\) は「ある時間 \(t\) 以上生存する確率」を表すものです。「誰がいつ死亡した」というデータから生存関数を推定する場合、死亡が観測された時間ごとに生存関数の値が小さくなっていくように推定された関数の形を決めるのは直観的に自然であると言えると思います。さらにそれに加えて、打ち切りが発生した場合には推定生存関数の値を小さくしないような力を加えたものが Kaplan-Meier 推定量であるというように理解することができます。
Nelson-Aalen 推定量
Nelson によって最初に提案され、その後 Aalen によって再発見された累積ハザード関数 \(H(t)\) の推定量 \(\tilde{H}(t)\) Nelson-Aalen 推定量と呼ばれ、以下のように定義されます:
$$\begin{align*}
\tilde{H}(t) = \left\{
\begin{array}{ll}
0 \displaystyle\frac{\mbox{}}{\mbox{}}& (\mathrm{if} \quad t < t_1) \\
\displaystyle\sum_{i = t_1}^t \frac{d_{i}}{Y_{i}} & (\mathrm{if} \quad t_1 \le t)\end{array}
\right.
\end{align*}$$
6-MPに対する Nelson-Aalen 推定量をプロットすると以下のようになります:
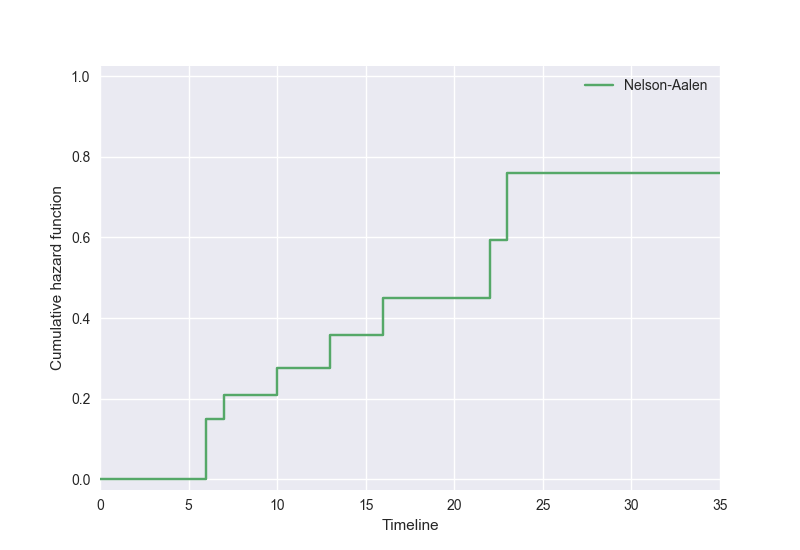
Kaplan-Meier 推定量と Nelson-Aalen 推定量で値が変化するタイミングは同じです。Nelson-Aalen 推定量は 0 からスタートして、誰かの死亡が観測された時点で値が大きくなるような階段関数です。
累積ハザード関数 \(H(t)\) は「ある時点 \(t\) 直前まで死亡していない上で \(t\) に死亡する確率」である \(h(t)\) を累積したものですから、生存関数とは逆に、死亡が観測された時間ごとに値が大きくなるような関数形になっているのもまた自然であると思います。
推定量の変換
前記事で述べた基本量の関係とも関連しますが、生存関数 \(S(t)\), ハザード関数 \(h(t)\), 確率密度関数 \(f(t)\), 累積ハザード関数 \(H(t)\) のような生存時間解析における基本量は、どれか一つが求まるとその他の関数も一意に求めることができます。 特に生存関数 \(S(t)\) と累積ハザード関数 \(H(t)\) の関係は以下のように表されます:
$$\begin{align*}
H(t) &= -\ln\left[ S(t) \right] \\
S(t) &= \exp\left[ -H(t) \right]
\end{align*}$$
これを Kaplan-Meier 推定量 \(\hat{S}(t)\) あるいは Nelson-Aalen 推定量 \(\tilde{H}(t)\) に関しても同様に適用すると、以下のようになります:
$$\begin{align*}
\hat{H}(t) &= -\ln\left[ \hat{S}(t) \right] \\
\tilde{S}(t) &= \exp\left[ -\tilde{H}(t) \right]
\end{align*}$$
つまり、
- Kaplan-Meier 推定量から導かれた累積ハザード関数 \(\hat{H}(t)\)
- Nelson-Aalen 推定量から導かれた生存関数 \(\tilde{S}(t)\)
が求まります*6。
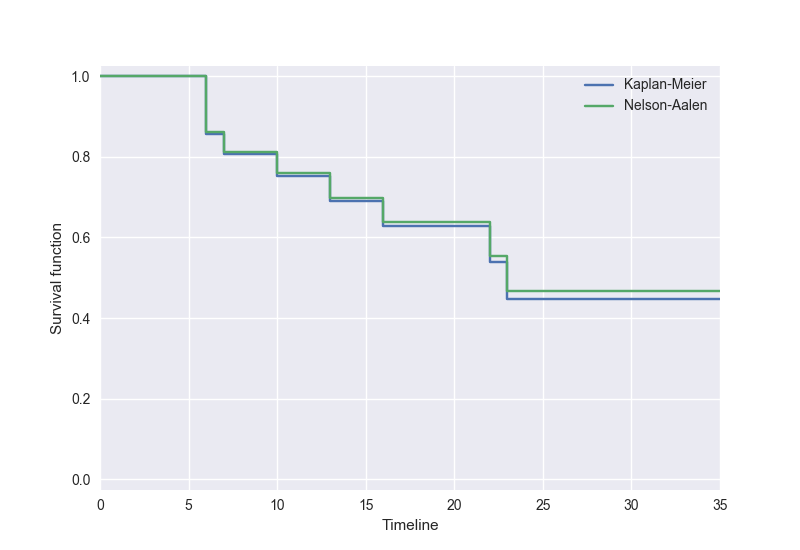
6-MPに対して、 Kaplan-Meier 推定量による推定生存関数 \(\hat{S}(t)\) と Nelson-Aalen 推定量による推定生存関数 \(\tilde{S}(t)\)を同時にプロットすると以下のようになります:
また、Kaplan-Meier 推定量による推定累積ハザード関数 \(\hat{H}(t)\) と Nelson-Aalen 推定量による推定累積ハザード関数 \(\tilde{H}(t)\) を同時にプロットすると以下のようになります:
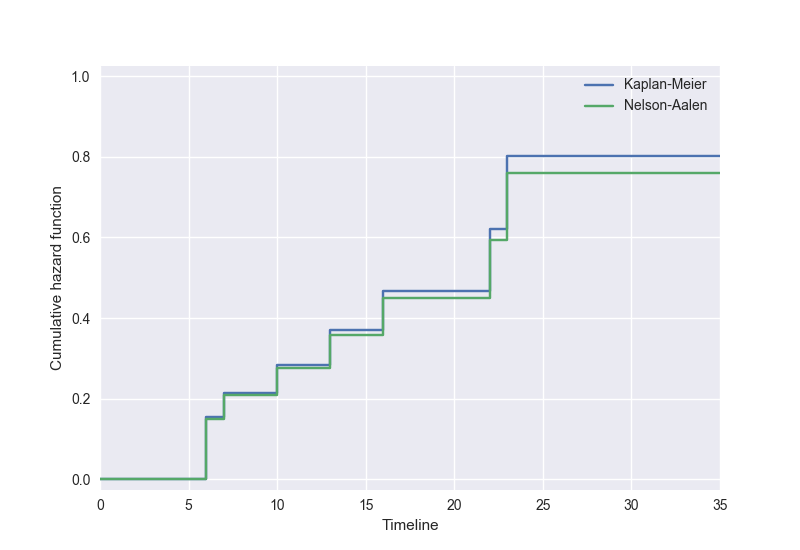
これらより、死亡のイベントが発生した時間に関数値が変化するという性質が常に保たれていることが確認できます。 異なる推定式から導かれた関数なので、当然関数値は異なります。Nelson-Aalen 推定量は Kaplan-Meier 推定量と比較して「小さいサイズの標本に対してよりよい性質をもつ」 [Klein and Moeschberger] とのことですが、ここでは詳細には触れないこととします。
おわりに
本記事では、生存時間解析におけるノンパラメトリックな推定量のうち代表的なものである Kaplan-Meier 推定量と Nelson-Aalen 推定量について非常に簡単に紹介しました。 最初に述べた通り、ノンパラメトリック推定は予測モデリングのニーズに応えることを想定した手法ではないため、この手法を直接転職可能性予測に組み込んでいるわけではありません。 参考までに、セミパラメトリックなモデルの一つであるCox比例ハザードモデルはノンパラメトリックなモデルとフルパラメトリックなモデルのハイブリッドともいえるものですが、そのノンパラメトリックな部分に関しては Kaplan-Meier 推定量の考え方が応用されています。 そのため、本記事をご覧いただいたことによってセミパラメトリックなモデルに関する理解を早めることができると思います。 今後はフルパラメトリックなモデル、セミパラメトリックなモデルに関する記事を公開する予定です。
参考文献
- [Friereich et al.] Freireich, Emil J., et al. "The effect of 6-mercaptopurine on the duration of steroid-induced remissions in acute leukemia: A model for evaluation of other potentially useful therapy." Blood 21.6 (1963): 699-716.
- [Klein and Moeschberger] Klein, John P., and Melvin L. Moeschberger. Survival analysis: techniques for censored and truncated data. Springer Science & Business Media, 2005.
脚注
*1: 例えば、薬効に関する分析であれば各患者、転職時期予測に関する分析であれば各候補者を指すようなものです。
*2: 例えば年齢や性別といった、個人ごとに異なる情報のことです。
*3: もちろん、そうでない文献も存在します。
*4: 特に、実世界の問題に対する予測モデリングのために生存時間解析の手法を応用する場合は、セミパラメトリックなモデル、あるいはフルパラメトリックなモデルを利用するのが適切でしょう。
*5: 「積-極限推定量」とも。
*6: \hat{} で Kaplan-Meier 推定量を、 \tilde{} で Nelson-Aalen 推定量をそれぞれ表しています。

